自由空間とは無限に広がる架空の空間のことで、アンテナや電波の特性を定義するために使われます。
地球上に存在する空間は、空気もあれば温度もありますよね。加えて、雨や風などの気象条件も揃っています。
自由空間には、これらが一切ありません。
一切無いので、電波は余計なものの影響を受けない状態で進むことができます。
つまり、電波にとって「この上ない条件」ということです。
ですが自由空間を進む電波も、性質上進む距離が長くなるにつれて段々と減衰します。
この度合いを表したものが自由空間基本伝送損失というもので、次の式で表されます。
$$\largeΓ_0=(\frac{4πd}{λ})^2$$

この式から、「アンテナ間の距離が長いほど」「波長が短くなるほど」損失が大きくなることが分かります。
一陸特の試験では、自由空間基本伝送損失が絡んだものとして、次のような問題が出題されます。
下の図は、マイクロ波回線の概略図である。
A局から送信機出力電力2[W]で送信したとき、B局における受信機の入力電力の値はおよそ何[dBm]か。
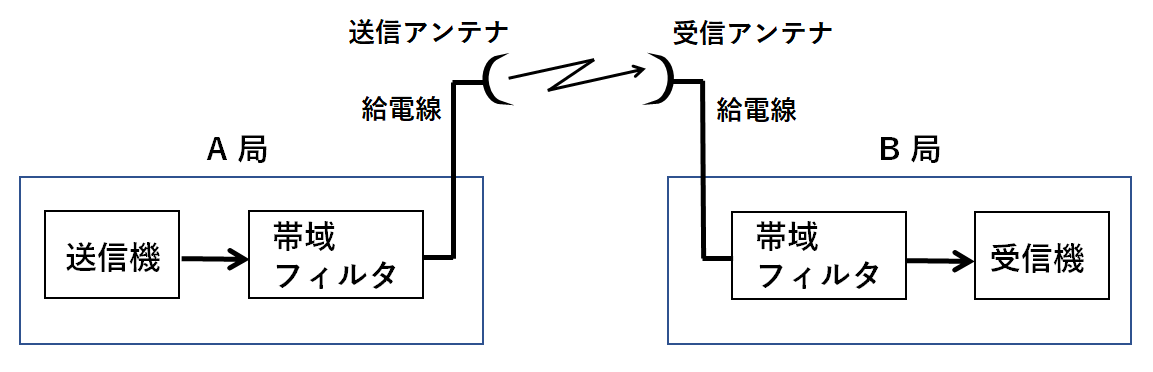
ただし、送信アンテナと受信アンテナの絶対利得をそれぞれ45[dB]、送信および受信帯域フィルタの損失をそれぞれ2[dB]、送信および受信給電線の長さをそれぞれ10[m]、給電線損失を0.3[dB/m]、自由空間基本伝送損失を130[dB]とし、1[mW]を基準(0[dBm])、\(log_{10}2\)=0.3とする。
問題文が長くて嫌になりそうですが、実は得点しやすい問題です。
というのも、与えられた各値と求めるべき値の単位がデシベル表記(dBm、dB)なので、順序よく足し算と引き算を繰り返していけば、最終的に答えにたどり着けるからです。
(デシベル関連の記事も参考にしてみてください)
------------------------
さて、今回はA局の送信機から電力が出ているので、ここがスタートです。
問題文を見ると、伝送路上の各物体は「利得」と「損失」のどちらかをもっていることが分かります。
これらを、その値と共に問題の図に書き入れてみました。
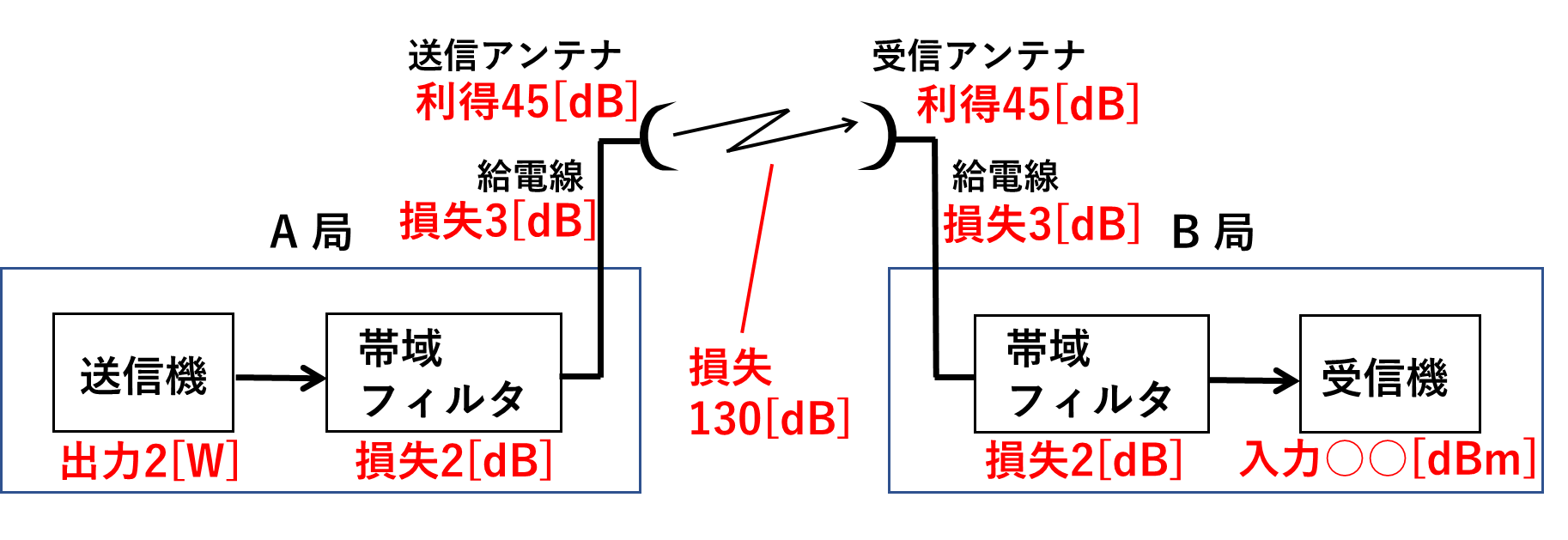
給電線の損失については、
問題文より給電線1mあたりの損失が0.3[dB]、給電線の長さが10[m]なので、
\(0.3\times10=3\)[dB]となります。
一般的に信号は、利得があるものを通過するとパワーアップし、損失があるものを通過するとパワーダウンします。
つまり、利得があるものを通過する時はその値を足し、損失があるものを通過する時はその値を引けば良いのです。
早速やってみましょう!
・・・と言いたいところですが、与えられた送信電力の単位が[W]になっています。
このままだと足し引きできないので、まずはこれをデシベルに換算する必要があります。
今回、1[mW]を基準としているので、
\(10log_{10}(2\times10^3)=10(log_{10}2+log_{10}10^3)\)
\(=10(0.3+3)=33\small[dBm]\)
(電力の単位をデシベルにしてみようより)
これで準備が整ったので、A局の送信機からB局の受信機まで、信号(電波)の伝送路に沿って計算していきます。
A局送信機の出力から・・・→A局帯域フィルタの損失を引く→A局給電線の損失を引く→A局送信アンテナの利得を足す→自由空間伝送損失を引く→B局受信アンテナの利得を足す→B局給電線の損失を引く→B局帯域フィルタの損失を引く=B局受信機の入力!
それぞれ数値を使って表すと、
33[dBm]-2[dB]-3[dB]+45[dB]-130[dB]+45[dB]-3[dB]-2[dB]=-17[dBm]
めでたく受信機の入力が求まりました!
------------------------
この手の問題で大切なことを下記にまとめます。
⭕送信している局と受信している局を把握
⭕伝送路中の「利得」と「損失」を漏れなくピックアップ
⭕デシベル表記になっていない値は換算する
⭕「利得」は足し算、「損失」は引き算
ちなみに求めるものに関しては、毎回受信入力とは限りません。
受信入力が与えられていて、自由空間基本伝送損失を求める場合もあります。
ですがどの場合も、上記で行ったように足し算引き算の式を立てて、最終的に(求めるもの=)の形にしてやればOKです。
最初は混乱するかもしれませんが、慣れると簡単に得点源にできるので、是非何度も繰り返してモノにしてください!