仮に二つの無線局同士で電波をやり取りしたい場合、この二つの間にビルや山(=障害物)が無いことは必須条件です。
なので新しく相手局を建てる時は、あらかじめ片方の無線局から相手局の候補地(の方向)を見て、障害物が無いかを確認するわけです。
障害物が全く無い場合を「見通せる」と表現したりします。
タイトルにもある見通し距離とは、ある無線局から見通せる場合の、相手局まで電波が進む距離です。
言葉だけだとわかり辛いので図にしてみました。

AとBはどちらも無線局で、これらの間には障害物が何も無い状態です。
特にマイクロ波を使う無線局を建てる場合、絶対に見通せる必要があります。
マイクロ波は直進性が高いので、間に山などがあっては話にならないからです。
一陸特の試験においても、この見通し距離を求める問題が登場しますが、ほとんどは公式を使って解く計算問題です。
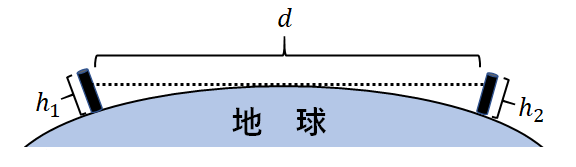
二つのアンテナの地上高をそれぞれ\(h_1\small[m]\)、\(h_2\small[m]\)とすると、このアンテナ間の見通し距離\(d\small[km]\)は、
●等価地球半径係数を1とした場合
\(d≒3.57(\sqrt{h_1}+\sqrt{h_2})\)・・・・(1)
●等価地球半径係数を\(\large\frac{4}{3}\)とした場合
\(d≒4.12(\sqrt{h_1}+\sqrt{h_2})\)・・・・(2)
で表される。
等価地球半径係数という訳のわからない言葉が出てきましたが、とりあえず今は無視して大丈夫です。
実際の問題は、例えばこんな形で出てきます。
送信アンテナの地上高を196[m]、受信アンテナの地上高を4[m]とする。
この時、送受信アンテナ間の電波の見通し距離はおよそいくらか。
ただし、大地は球面とし、標準大気における電波の屈折を考慮するものとする。
最後のただし書きがいやらしいですよね(笑)。
何かひっかけがあるのではと思ってしまいますが、このように書いてある場合は、上記の(2)式(等価地球半径係数を\(\large\frac{4}{3}\)とした場合)の方を使います。
そのまま値を代入すると、
\(d≒4.12\times(\sqrt{196}+\sqrt{4})\)
\(=4.12\times(14+2)\)
\(=4.12\times16\)
\(=\)\(65.92\small[km]\)
このようにして見通し距離が求められます。
一陸特の取得に重きを置いた話になって恐縮ですが、「等価地球半径係数を\(\large\frac{4}{3}\)とする」とか「標準大気における電波の屈折を考慮する」といった言葉が書いてある場合は、(2)式が関係していると思ってください。
なおアンテナ地上高は、電卓が使えない分、計算しやすい数値が与えられているので、式さえ覚えていれば大丈夫です。
----------------------------
さて、先程スルーした等価地球半径係数ですが、これは見通し距離をスムーズに求めるために導入されたものになります。
等価地球半径と見通し距離の関係で紹介しています。