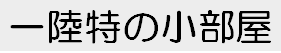見通し距離の求め方では、一陸特の試験にも出る見通し距離の計算方法について紹介しました。
ここでは、見通し距離と関係が深い等価地球半径について、少し補足したいと思います。
-------------------------
普段私達が実感することはありませんが、地球は丸いので、大地も湾曲しています。
そして、特に中波以下(3MHz以下)の周波数の電波は、この湾曲した地表面に沿って進みます。
このような進み方をする電波は「地表波」と呼ばれます。

ただ、新しく無線局を作ったりする場合は、電波はまっすぐ進んだ方が何かと都合が良くなります。
というのも地表に沿った進み方だと、例えばある送信所の相手局を建てる場所を選定したい場合、その送信所から放射される電波の経路上に障害物があるか無いかが、わからないんですよね。
地球は丸いので、障害物の有無が確認できるのは地平線までです。
そこで博識な人達は、電波が曲がる性質をもっていても計算しやすいように、地球の半径をもう少し大きいものと仮定しました。
送信所の位置はそのまま、電波の進み方もそのままで、地球の半径だけ大きくする状態です。
風船が段々膨らんでいく状況をイメージしてください。
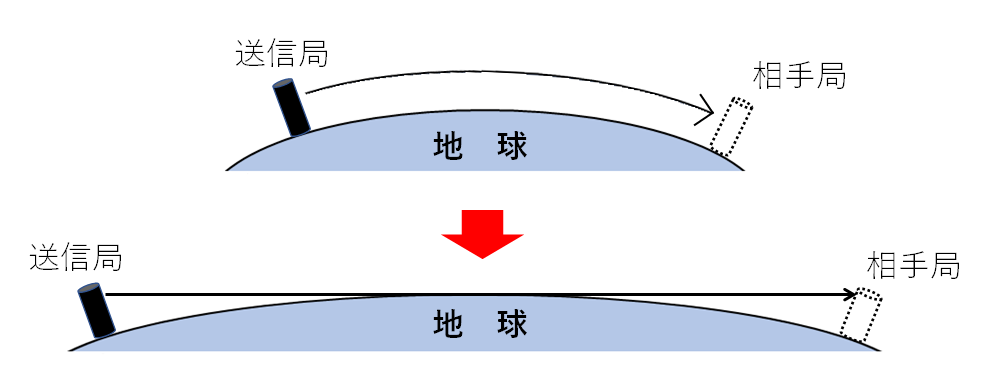
そうすると、曲がっていた電波の経路も段々まっすぐになります。
さて問題は、地球の半径をどれだけ大きくするかですよね。
これについては、半径を元の\(\large\frac{4}{3}\)倍にします。
こうすることで、電波の経路が直線とみなせるようになるのです。
この\(\large\frac{4}{3}\)が等価地球半径係数で、アルファベットの\(K\)で表します。
「半径を何倍にしたか」なので、\(K=1\)だと、元の地球の半径と同じ(何も変えていない)ということです。
最後に、別記事でも紹介した見通し距離を求める式を、あらためて書いておきます。
●等価地球半径係数を1とした場合
\(d≒3.57(\sqrt{h_1}+\sqrt{h_2})\)
●等価地球半径係数を\(\large\frac{4}{3}\)とした場合
\(d≒4.12(\sqrt{h_1}+\sqrt{h_2})\)
で表される。
等価地球半径係数が何者かわかりましたでしょうか?
一陸特の問題では上記の二式をよく使いますが、どちらの式を使うかは問題文にただし書きがあるので、そちらを参考にしてもらえればと思います。