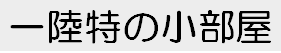山岳回折とフレネルゾーンでは、ナイフエッジによる回折波と直接波の干渉や、それが起こるフレネルゾーンという領域について紹介しました。
このフレネルゾーンの概念は、マイクロ波の回線を設計する際になくてはならないものです。
例えば、街中に新しく送信局と受信局を建てたいとします。
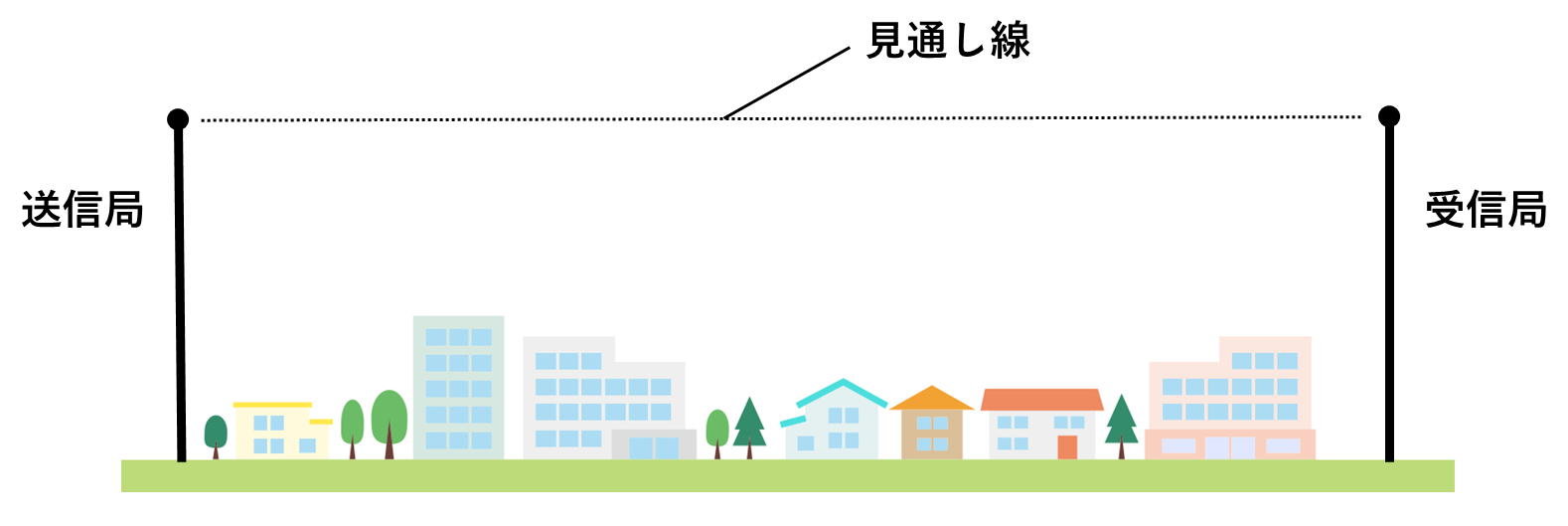
上図の見通し線とは、送信局と受信局がそれぞれ電波を出す点(=送信点と受信点)を結ぶ直線のことです。
この2つの点を焦点とした楕円を描いた時、楕円の内側の領域が「第1フレネルゾーン」となります。

大切なのは、回線を設計する際は、建物などの障害物が第1フレネルゾーンの領域に入らないようにすべきということです。
もし障害物が入った状態だと、その影響で受信局の電解強度が時間的に強弱を繰返し(=フェージング)、通信の安定性が損なわれる恐れがあるからです。
なお、こういった障害物と見通し線との距離を「クリアランス」といいます。
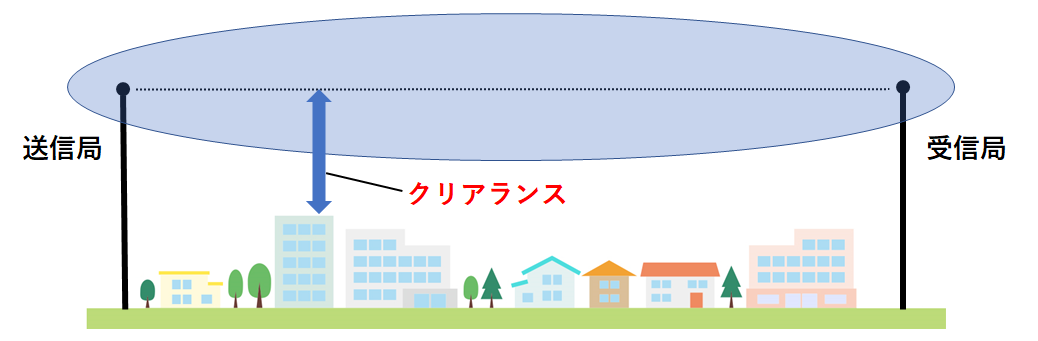
充分なクリアランスをとることで安定した通信が可能となりますので、もし将来マイクロ回線などの設計担当になった暁には、意識してもらえたらと思います。
フレネルゾーンの半径
今更で申し訳ないですが(笑)、上で紹介したフレネルゾーンは、左右だけではなく奥行きをもっています。
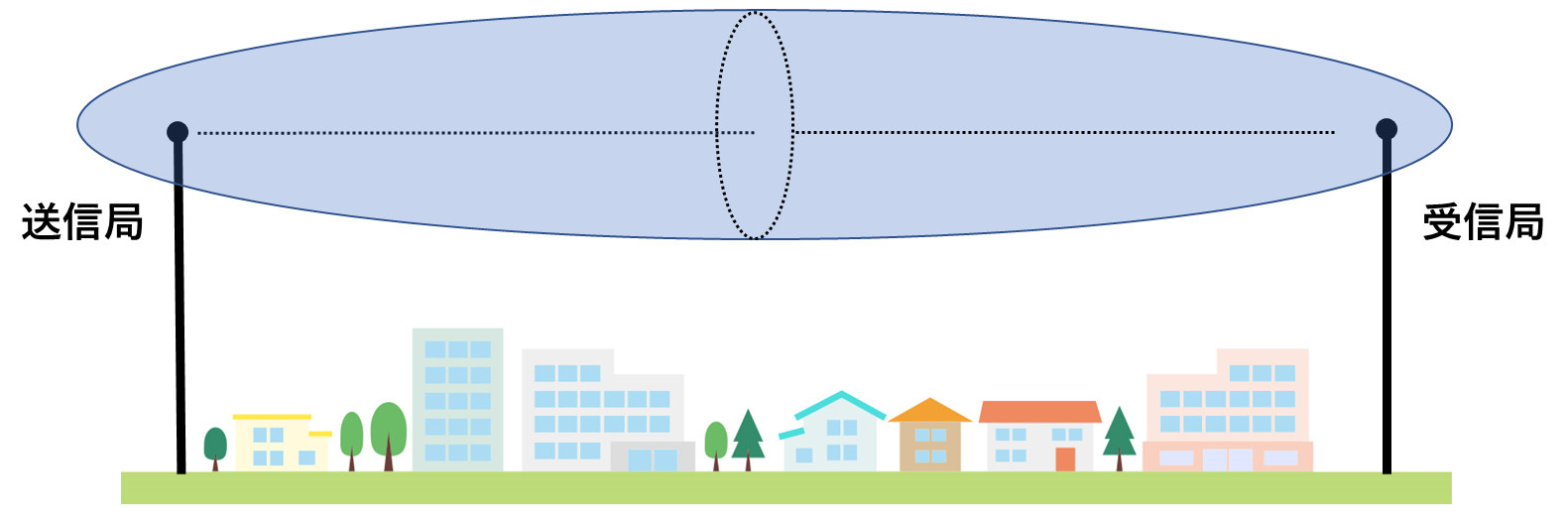
イメージとしては、少し横長のラクビーボールがかぶさっているような状態ですね。
この半径を求める式も一陸特の試験に登場するので、併せて紹介しておきます。
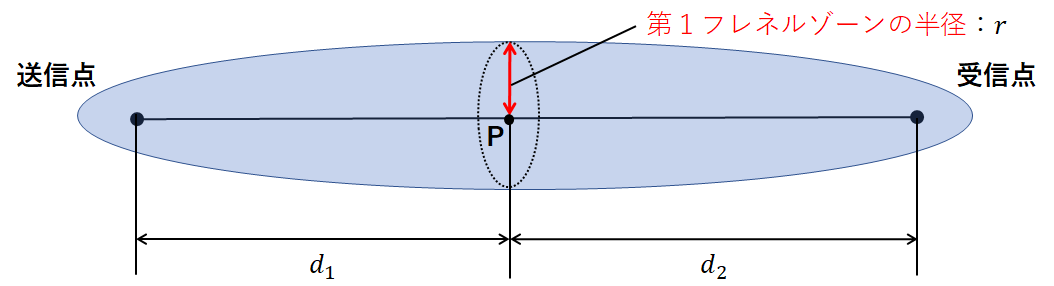
送信点からの距離が\(d_1\small[m]\)、受信点までの距離が\(d_2\small[m]\)の点Pにおける第1フレネルゾーンの半径\(r\small[m]\)は、電波の波長を\(λ\small[m]\)とすると、
$$r=\sqrt{\frac{λd_1d_2}{d_1+d_2}}$$
で表される。
この式を使えば、例えば\(d_1\)が8[km]、\(d_2\)が12[km]、周波数が6[GHz]で与えられた場合、
波長\(λ=\)\(\Large\frac{3\times10^8}{6\times10^9}\)\(=5\times10^{-2}
\small[m]\)なので、
フレネルゾーンの半径\(r\)は、
\(r=\)\(\Large\sqrt{\frac{5\times10^{-2}\times8\times10^3\times12\times10^3}
{8\times10^3+12\times10^3}}\)
\(=\)\(\Large\sqrt{\frac{480\times10^4}
{20\times10^3}}\)\(=\sqrt{240}≒15.5\small[m]\)
と求めることができます。
たまに\(d_1\)か\(d_2\)のどちらかしか与えられてない場合もありますが、その代わりに送信点から受信点までの距離が与えられていますので、これから\(d_1\)を引けば\(d_2\)が、\(d_2\)を引けば\(d_1\)がそれぞれ分かりますね。
計算以外では、式そのものが選択肢に登場する場合もあります。
間違いの選択肢は、例えば次のように形を変えて書かれています。
●ルートが無い
●分子の掛け算に\(λ\)が含まれていない
●足し算と掛け算が逆
特に分母と分子の形を逆に覚えたりしがちなので、正しい式の特徴を頭に入れておいてください。