最小探知距離とは、レーダーと対象物間の距離の中でも、レーダーが対象物を探知可能な最短距離のことです。
これには、レーダーが出すパルスの幅、いわゆるパルス幅が関係しています。
幅といっても長さのことではなく、下図に示すようにパルスの右端が通過した点を、同じパルスの左端が通過するまでの時間を指しています。
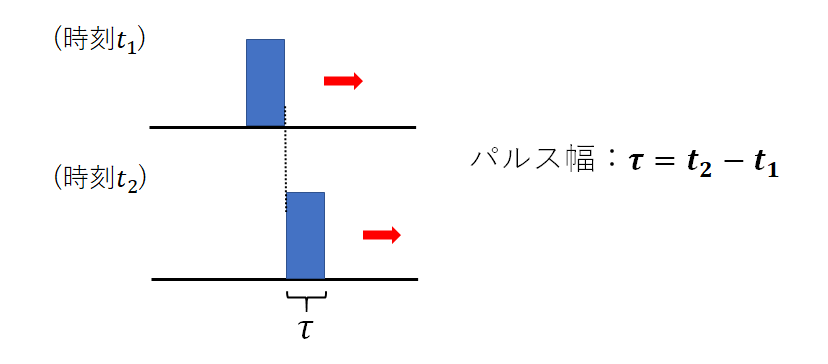
パルス幅を表す記号には\(τ\)(タウ)が、単位は\(\small[μs]\)が使われます。
上の図はわかりやすいようパルスを大きめに書いていますが、ある地点をパルスが通過するのは一瞬の出来事なのです。
--------------------------------
あまり馴染みのないパルス幅ですが、実はこれを使うと最小探知距離が簡単に求まるので、少し説明します。
繰り返しになりますが、パルス幅とはパルスの右端が通過した点を、同じパルスの左端が通過するまでの時間でした。
これは言い替えれば、レーダーがパルスを産み出している最中、つまり「送信中」の時間です。
送信中ですから、この間、対象物からパルスが返ってきても受信はできません。
この場合の、「レーダーのアンテナ」から対象物までの距離を\(R\)、電波の速度を\(c\)、パルス幅を\(τ\)としましょう。
対象物を探知するためには、レーダーから出したパルスがこの距離を往復しなければならないので、「距離=速さ\(\times\)時間」の公式より\(2R=c\largeτ\)が成り立ちます。
この式の両辺を2で割ると、
\(R=\Large\frac{cτ}{2}\)・・・・・(1)
よって、この距離が「対象物を認知できる最も短い距離」すなわち「最小探知距離」となります。
レーダーから対象物までの距離は、少なくともこの距離以上でないと探知できません。
さらに、電波は光の速さと同じなので\(c=3\times10^8\small[m/s]\)、パルス幅を仮に\(τ\times10^{-6}\small[s]\)として(1)式に代入すると、
\(R=\Large\frac{cτ}{2}=\Large\frac{3\times10^8\timesτ\times10^{-6}}{2}\)
\(=150\largeτ\)・・・・・(2)
結果的に、最小探知距離は150と\(τ\)の積で求めることができます。
なお、最小探知距離に関する問題としては、
●「パルス幅が与えられていて、最小探知距離を求める」
●「最小探知距離が与えられていて、パルス幅を求める」
大体このどちらかです。
特に(2)式の場合、最小探知距離は\(150\timesτ\)、パルス幅は\(\large\frac{R}{150}\)で計算できるので、かなり楽です。
(1)式は速さ(\([m/s]\))との掛け算なので、単位を打ち消しあう必要があるからです。
ちなみに、レーダーの距離分解能も、同じ式で求めることができます。
計算問題の類いになりますが、公式が単純な形なので是非覚えておいてください。