↑こんな形のアンテナ、見たことがある方もいらっしゃるのではないでしょうか。
パラボラアンテナは主に3GHz~30GHzの周波数を用いた通信に使われ、「一次放射器」と「放物面反射鏡」メインで構成されています。

送信時は、まず一次放射器から放物面反射鏡に向かって電波が放射されます。
放物面反射鏡に到達した電波はそれぞれの地点で反射しますが、どの位置で反射した電波も、任意の地点(例えば下図の「a」)まで進んだ距離は同じになります(これは、一次放射器が反射鏡の焦点に設置されているからです)。
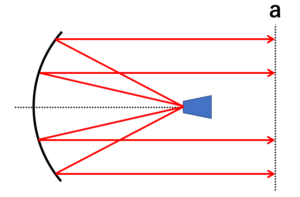
結果的に、パラボラアンテナからは位相が揃った平面波が放射されるので、鋭い指向性と、高い利得を併せ持つようになります。
利得とは、アンテナの性能を示すためにしばしば用いられるもので、パラボラアンテナの場合、次の式で表すことができます。
$$G=\frac{4πA}{λ^2}η$$
![]()
利得は「絶対利得」であることに注意してください。
利得といってもなかなかイメージし辛いですが、「電波を送受信する際の効率の良し悪しを表すもの」と思って頂けたら幸いです。
(利得の記事も参考にしてみてください)
---------------------------------
ここで、上の式に関係した計算問題をやってみましょう。
21[GHz]の周波数の電波で使用しているパラボラアンテナがある。
放物面の開口面積が0.4[\(m^2\)]、絶対利得が40[dB]のとき、このパラボラアンテナの開口効率はおおよそ何%か。
波長は、光速[m/s]を周波数[Hz]で割ると求められます。
今回、周波数が21[GHz]なので波長\(λ\)は、
\(λ=\Large\frac{3\times10^8}{21\times10^9}\)
\(=\Large\frac{1}{7}\)\(\times10^{-1}≒0.143\times10^{-1}\)
ここで注意したいのが、先程の\(G=\frac{4πA}{λ^2}η\)で表される絶対利得\(G\)です。
この\(G\)は「真数値」です。
一方で、問題文の絶対利得はデシベル表記になっているので、そのまま関係式には代入できません。
デシベル表記を真数表記になおす必要があります。
これについては、与えられた数値を対数の式に当てはめると、
\(40=10\log_{10}G\)
よって、これを満たす真数\(G\)の値は\(10^4\)となります。
(このあたりの話は、一陸特対策に欠かせない対数についてでも扱っているので、参考にしてください。)
ここまでできたら、絶対利得の式を\(η=\)の形にして、値を代入すれば求められます。
\(η=\Large\frac{Gλ^2}{4πA}=\frac{10^4\times(0.143\times10^{-1})^2}{4\times3.14\times0.4}\)
\(≒\Large\frac{2.045}{5.024}\)\(≒0.407\)
よって、開口効率はおよそ40[%]となります。
---------------------------------
パラボラアンテナについて簡単に紹介しましたが、実はこのアンテナ、反射鏡の真正面に一次放射器が設置されているため、電波の進行が妨げられやすくなっています。
これを防ぐために開発されたアンテナが「オフセットパラボラアンテナ」です(別記事で紹介しています)。